The two beams will be made up of cylinder-like bunches 7.48 cm long and ~ 16x16 micras section (1 millimetre wide when they are far from a collision point).

a) Let's calculate the repulsion force between near protons in the interaction point.

The "volume occupied" for each proton is:

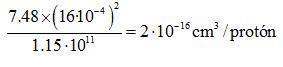
The radius of this volume is:    r ~ 5·10^-6 cm

so the distance between near protons is:  d = 2·r  →  d ~ 10^-5 cm.

According to the Coulomb law repulsion between nearest protons is:

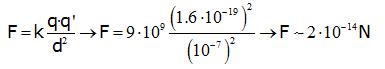
b) We can also calculate the repulsion force between near protons far from a collision point.

In that case the section is over 1 mm², so the "volume occupied" for each proton is bigger so the force is smaller .

The "volume occupied" for each proton in that case is:

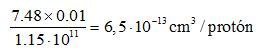
The radius of this volume is:    r ~ 5·10^-5 cm

so the distance between near protons is:  d = 2·r  →  d ~ 10^-4 cm.

According to the Coulomb law repulsion between nearest protons is:

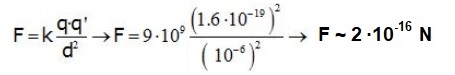
Due to the very small mass of each proton the effect caused for that forces would be important. So the beam has to be permanently focussed. This is achieved by quadrupole magnets, which act on the beam of charged particles exactly the same way as a lens would act on a beam of light.

Let´s calculate the total electrical charge for each bunch. Q = 1,602·10-19 x 1,15·1011 = 18,4 nC Let´s imagine each bunch as one compact charged object.Each bunch repels the one in front and behind according to the Coulomb law. F = 9·109·(18,4 ·10-9)2 / (7,48)2 F = 5,45·10-8 N

Due to the very small mass of each bunch the effect would be important but forces cancel themselves out. However the configuration is not completely symetric so little by little instabilities are generated limiting the life span of the beam (“Beam lifetime”) which doesn´t exceed 10 hours functioning.

The beam current is the basic quantity of the beam and and a simple approximation can be seen in this page.  But for didactical intnetion we can calculate the circulating current beam from the number of protons per bunch. The total number of protons in each beam is: N = 2808 · 1,15·1011 = 3,23·1014 protons So, in one second (11245 laps), the total charge inside each pipe per sec: Q = 3,23·1014 · 1,602·10-19 · 11245 = 0,58 Culomb Therefore,the Intensity will be,   I = 0,58 Amperes - Important accelerator parameter -