Taking a closer look at LHC
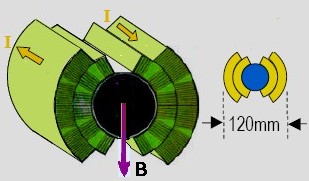
| The dipolar magnetic field is created for superconductive currents which circulate on each side of the pipe by where the protons travel. The wiring is arranged in individual double layers around each tube, circulating in opposite senses on each side. Since the pipe is 56 mm diameter, we take, according the image, 45 mm as average distancia betwen the cables andthe center of pipe. |
 |
|
The fields arising from current sources in the coil are calculated analytically by means of the Biot-Savart law. As it's been stated before, the average distance from de cables (cooper colour in the image) to the pipe centrer is roughly 45 mm. B = μ0·I/(2πd) With I ~11800 A and r = 45 mm ⇒ B ~ 0.05 T Since we need B = 8.33 T , 8.33/0.05 ~ 160 cables
|
 |
So to reach 8.33 T, in the first approximation, we would need 160 superconducting cables. Eighty cables placed in two layers go parallel to the beam pipe axis and back on the other side.
The cables house 36 strands of superconducting wire, each strand being exactly 0.825 mm in diameter. Each strand houses 6500 superconducting filaments of Niobium-titanium (47Wt% Ti).
Each dipole is15 m long, so we can calculate the total superconducting length in the 1232 dipoles (2 tubes per dipole):
L = 2 x 1232 x 160 x 36 x 6500 x 15 ⇒ L = 1,38·1012 m
This value is 9 times the distance Sun - Earth. If we consider the superconducting cable for the other multipoles and the magnetic systems of the detectors, we get mora than 10 times that distance.
|
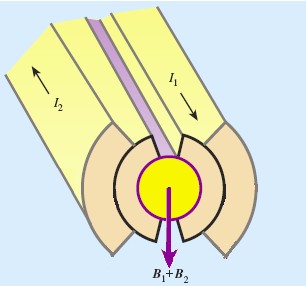
Since the current direction for each set of cables has to be opposite to the other set, the same vector B perpendicular to pipe axis is achieved. A similar disposition has to be considered for the other pipe but in the opposite sense. This is the configuration 2-in-1. |
 |
|
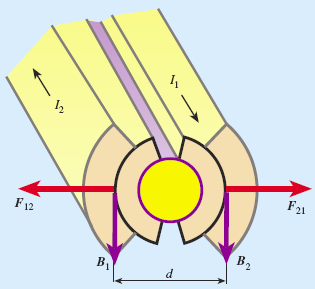
We know that attractive or repulsive forces are generated between parallel conductors according to the direction of their currents. As it’s been said, currents go in an opposite sense in each dipole so there will be repulsive forces between each couple of cable sets. We can use the next approximation to calculate this force from the known formula:
F/L =μ0·I1··I2/(2πd) With I ~11800 A and d = 90 mm, F/L = 310 N/m
|
 |
|
But we have two sets of 80 cables, so the total force per meter will be:
FT = 80·80·310 ~ 2·106 N/m Due the geometrical design of the coil, that force will affect mainly the horizontal direction but will also affect the other ones.
It’s a very strong force which tends to “open” the magnet. To counteract this force, engineers contained the conductors that carry the electrical current with collarsmade out of non-magnetic stainless steel material. A yoke made of iron, a magnetic material, surrounds these non magnetic collars.
|
 |
We can calculate the Dipole Inductance.
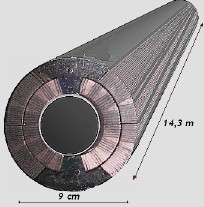
Let’s consider a cylindrical coil (14,3 m long and 9 cm wide on average) with 80 turns and a perpendicular magnetic field 8,33 T.
| The magnetic Flux throughout the surface is:
φ = N·B·S ⇒ φ = 80·8,33·(14,3·0,09) φ ≈ 1000 Wb With, φ = L·I L = 1000/11800 ⇒ L ≈ 0.1 H So the stored energy is: Ed = ½·L·I2 ⇒ Ed ≈ 7 MJ Considering 1232 dipoles: ET ≈ 9 GJ Enough to melt completely 45 tons of Gold from 25 ºC.
|
 |
If we consider the dipole lenght, the energy density of the LHC main dipole is:
7000/14,3 ≈ 500 kJ/m
After 10 h of beam collisions, the beam itself is exhausted and is dumped. The dipole magnets are then ramped down to 0.54 T and they stay at flat bottomfor some 20–40 min. Meanwhile beam injection is repeated before the magnets are ramped up again to 8.3 T for another cycle of high energy collisions. The machine is designed to withstand some 20 000 such cycles in 20 years’ lifetime.
Comparison of dipoles from the Tevatron to the LHC.
Taken from: Lucio Rossi (2011): Superconductivity and the LHC: the early days
|
AUTHORS Xabier Cid Vidal, PhD in experimental Particle Physics for Santiago University (USC). Research Fellow in experimental Particle Physics at CERN from January 2013 to Decembre 2015. He was until 2022 linked to the Department of Particle Physics of the USC as a "Juan de La Cierva", "Ramon y Cajal" fellow (Spanish Postdoctoral Senior Grants), and Associate Professor. Since 2023 is Senior Lecturer in that Department.(ORCID). Ramon Cid Manzano, until his retirement in 2020 was secondary school Physics Teacher at IES de SAR (Santiago - Spain), and part-time Lecturer (Profesor Asociado) in Faculty of Education at the University of Santiago (Spain). He has a Degree in Physics and a Degree in Chemistry, and he is PhD for Santiago University (USC) (ORCID). |
CERN CERN Experimental Physics Department CERN and the Environment |
LHC |
IMPORTANT NOTICE
For the bibliography used when writing this Section please go to the References Section
© Xabier Cid Vidal & Ramon Cid - rcid@lhc-closer.es | SANTIAGO (SPAIN) |



